What is GCM?
GCM is a block cipher mode of operation providing both
confidentiality and data origin authentication; It is defined for block
ciphers with block sizes of 128, 192 and 256 bits. Galois Message
Authentication Code (GMAC) is an authentication-only variant of the GCM
which can be used as an incremental message authentication code. Both
GCM and GMAC can accept initialization vectors of arbitrary length.
Who invented GCM?
GCM was designed by McGrew and Viega as an improvement to Carter-Wegman Counter CWC mode. On November 26, 2007 NIST announced the release of NIST Special Publication Recommendation for Block Cipher Modes of Operation: Galois/Counter Mode (GCM) and GMAC making GCM and GMAC official standards.
These are the Inputs and Outputs for GCM system
GCM has two operations, authenticated encryption and authenticated decryption, where the authenticated encryption has four inputs, and each of which is a bit string:
- A secret key K, whose length depends of the block cipher use.
- An initialization vector IV, that can have any number of bits between 1 and 2 ^64. For a fixed value of the key, each IV value must be distinct. If you are looking for efficiency is recommended 96-bit IV values.
- A plaintext P, which can have any number of bits between 0 and 2 ^39 -256.
- Additional authenticated data (AAD), which is denoted as A, this data is authenticated, but not encrypted, and can have any number of bits between 0 and 2 ^64.
There are two outputs:
- A ciphertext C whose length is exactly that of the plaintext P.
- An authentication is denotated as T, whose length can be any value between 0 and 28. The length is denotated as t.
How does It work?
First we have to know the notation
The two main functions used in GCM are block cipher encryption and multiplication over the field GF(2 ^128). The block cipher encryption of the value X with the key K is denoted as E(K, X). The multiplication of two elements X, Y ∈ GF(2 ^128) is denoted as X · Y , and the addition of X and Y is denoted as X ⊕ Y . A, the addition in this field is equivalent to the bitwise exclusive-or operation.
The function len() returns a 64-bit string containing the nonnegative integer describing the number of bits in its argument, with the least significant bit on the right. The expression 0l denotes a string of l zero bits, and AkB denotes the concatenation of two bit strings A and B. The function MSBt(S) returns the bit string containing only the most significant (leftmost) t bits of S, and the symbol {} denotes the bit string with zero length.
Now Let's know how it works...
Encryption
Let n and u denote the unique pair of positive integers such that the total number of bits in the plaintext is (n − 1) 128 + u, where 1 ≤ u ≤ 128.
The plaintext consists of a sequence of n bit strings, in which the bit length of the last bit string is u, and the bit length of the other bit strings is 128. The sequence is denoted P 1, P 2, ...,P n-1, P ∗ n, and the bit strings are called data blocks, although the last bit string, P ∗ n, may not be a complete block. Similarly, the ciphertext is denoted as C 1, C 2,...,C n − 1 ,C ∗ n, where the number of bits in the final block C ∗ n is u. The additional authenticated data A is denoted as A 1, A 2,..., A m − 1, A ∗ m, where the last bit string A ∗ m may be a partial block of length v, and m and v denote the unique pair of positive integers such that the total number of bits in A is (m − 1) 128 + v and 1 ≤ v ≤ 128.
The authenticated encryption operation is defined by the following equations:
The plaintext consists of a sequence of n bit strings, in which the bit length of the last bit string is u, and the bit length of the other bit strings is 128. The sequence is denoted P 1, P 2, ...,P n-1, P ∗ n, and the bit strings are called data blocks, although the last bit string, P ∗ n, may not be a complete block. Similarly, the ciphertext is denoted as C 1, C 2,...,C n − 1 ,C ∗ n, where the number of bits in the final block C ∗ n is u. The additional authenticated data A is denoted as A 1, A 2,..., A m − 1, A ∗ m, where the last bit string A ∗ m may be a partial block of length v, and m and v denote the unique pair of positive integers such that the total number of bits in A is (m − 1) 128 + v and 1 ≤ v ≤ 128.
The authenticated encryption operation is defined by the following equations:
Successive counter values are generated using the function incr(), which treats the rightmost 32 bits of its argument as a nonnegative integer with the least significant bit on the right, and increments this value modulo 2 ^32. More formally, the value of incr(F||I) is F||(I + 1 mod 2 ^32).
The function GHASH is defined by GHASH(H,A,C) = X m + n + 1, where the
inputs A and C are defined as we defined in the beginning, and the
variables X i for i = 0,...,m + n + 1 are defined below:
Below we can see the process of encryption.
Decryption
The authenticated decryption operation is similar to the encrypt operation, but with the order of the hash step and encrypt step reversed, as you can see below how it works by the following ecuations:
Multiplication in GF(2 ^128)
The multiplication operation is defined as an operation on bit vectors in order to simplify the specification, this corresponds to the particular field representation used in GCM. Each element is a vector of 128 bits, the i th bit of an element X is denoted as X i; The leftmost bit is X 0, and the rightmost bit is X 127.
The multiplication operation uses the special element R = 11100001 || 0 ^120; The function rightshift() moves the bits of its argument one bit to the right, in other words whenever W = rightshift(V), then W i = V i-1 for 1 ≤ i ≤ 127 and W 0 = 0. We can see it illustrated below.
The Field GF(2 ^128)
A finite field is defined by its multiplication and addition operations. These operations obey the basic algebraic properties that one expects from multiplication and addition (commutativity, associativity, and distributivity). Both operations map a pair of field elements onto another field element. In a polynomial basis,the multiplication of two elements X and Y consists of multiplying the polynomial representing X with the polynomial representing Y, then dividing the resulting 256-bit polynomial by the field polynomial; the 128-bit remainder is the result. GCM uses the following polynomial:
The addition of two elements X and Y consists of adding the polynomials together, because each coefficient is added independently, and the coefficients are in GF(2), this operation is identical to the bit wise exclusive-or of X and Y. No reduction operation is needed. Subtraction over GF(2 ^128) is identical to addition, because the field GF(2) has that property.
Attacks known
I find some information about his weaknesses in the GMAC (Galois Message
Authentication Code), well actually this is a common weak in all kind of encryption or decryption that needs a key. You have to use a value relative prime.
Sources:














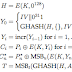



Faltó incluir un ejemplo. Ojo con la gramática. Van 5 pts.
ResponderEliminar