B.12.2. Sea el sistema definido por
donde
Transforme las ecuaciones del sistema en la forma canónica observable.
1. Se tiene el planteamiento del problema original (1.1) y (1.2).
2. Se crea la función de transferencia del sistema de control (2).
3. Se crea la forma normal controlable apartir de su función de transferencia (3.1) y (3.2).
4. Se hace la transpuesta de la forma normal controlable y cambio de variables de B a C
y de C a B, esto se hace para obtener la forma normal observable (4.1) y (4.2).
5. Al final verificamos que haya sido la misma función de transferencia(5).
Código en Octave:
El uso del código en octave y la verificación de que sean equivalente las funciones de tranferencia de cada forma usada:
Fuentes de ayuda:
http://www.engr.mun.ca/~millan/6825/canonicals.pdf











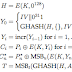




Muy bien; 15.
ResponderEliminar