Introducción
El sistema que se pretende controlar es el mismo que se tiene como proyecto final de esta materia. Para ello daré una breve explicación, mi proyecto trata de mover una pelota a cierta altura en el aire dentro de un tubo donde este será movido por un ventilador con un motor DC, gracias a un sensor ultrasonico este sabría hacia que altura moverse, osea que tanta potencia le daríamos al motor DC para que la pelota se eleve. Para ello reciclaremos el juguete que vemos abajo, conectando el motor DC y el sensor ultrasonico a un arduino que por medio de este haremos el control.
Reporte
Esta es su representación en la forma normal controlable.
Código en Octave:
Esta es su representación en la forma normal observable.
Código en Octave:
Esta es su representación en la forma de Jordan.
Código en Octave:
Código en Latex del documento:
Personas del equipo:
Saúl Gausin
Raúl Gonzalez
Isaías Garza
Suscribirse a:
Enviar comentarios (Atom)








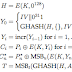



La idea era hacer un sólo reporte contínuo, incluyendo en ello los códigos y la explicación. No omiten acentos al redactar en español; se considera mala ortografía. Algunos de los bolas de derivada encima de los símbolos son absolutamente enormes o_0 Entre tres personas, esperaría más de un reporte. Explicación, referencias, etc. Van 15 pts.
ResponderEliminar