In this task I make a simulation of a channel, where transmit a word by a channel and a receptor receive the word and the word could come with some noisy like errors of the word. The program was made in Python making different methods, simulator() (Simulator make all the logic of the channel), generador() (generator of a letter of the word to send in the channel), palabra() (gets the word by a large) and transmisor() (It's the transmissor that sends the words by the channel). You can see my code below.
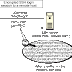
And with the help of a batch, awk and gnuplot I made a graphic of the output of the program.
This is the graphic where the axis x is the frequency of zero, axis y is the probability of ones, axis z is the probability of zero. The heat map represent the probability of success.
Suscribirse a:
Enviar comentarios (Atom)













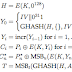



Bien. Al variar las variables, es un poco ineficiente:
ResponderEliminarfor fz in xrange(n):
for pz in xrange(n):
for pu in xrange(n):
freq_cero = ( fz * 1.0 ) / ( n * 1.0 )
prob_cero = ( pz * 1.0 ) / ( n * 1.0)
prob_uno = ( pu * 1.0 ) / ( n * 1.0)
mejor así:
for fz in xrange(n):
freq_cero = ( fz * 1.0 ) / ( n * 1.0 )
for pz in xrange(n):
prob_cero = ( pz * 1.0 ) / ( n * 1.0)
for pu in xrange(n):
prob_uno = ( pu * 1.0 ) / ( n * 1.0)
para no recalcular el valor de forma redundante.
Van 5+5.