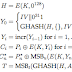Problema de laboratorio

P2.16.  Obténgase un grafo de flujo de señal para representar el siguiente conjunto de ecuaciones algebraicas donde yse consideran las variables dependientes y 6 y 11 son las

entradas:

Determínese el valor de cada variable dependiente usando la fórmula de la ganancia. Después, resuélvase para  mediante mediante la fórmula de ganancia del flujo de señal de Mason y verifíquese la solución usando la regla de Cramer.

Grafo de flujo de señal:

Ganancia del flujo de señal:

Regla de Cramer:

Reporte de Proyecto

Introducción

Para el reporte de la entrega final de proyecto explicaré denuevo de que trata mi proyecto, la idea del proyecto fue hacer una red neuronal que por medio de unos electrodos en el antebrazo de una persona determine los movimientos que quiere realizar en el brazo, esto se puede por medio de frecuencias que manda el cerebro hacia el brazo, y lo que se busca es interceptar esas frecuencias en el antebrazo para poder controlar un brazo robótico.

Al final se optó por usar un EEG debido a problemas con la Aduana al creer que los eléctrodos del sensor de músculo se podían tomar.

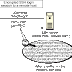
Donde podemos ver en la imagen de lado derecho separado por comas lo siguiente: "Intensidad de señal, atención, meditación, delta, theta, low alpha, high alpha, low beta, high beta, low gamma, high gamma".

Componentes

Los componentes que se usaron en el proyecto son los siguientes:

Arduino

EEG

Brazo robótico

MotorShield

¿ Cómo funciona?

Primero se toman las entradas del EEG para que luego sean preprocesadas, en el preprocesamiento se limpian los valores que nos importan donde mala intensidad de señal se ignora.

Al final obtenemos los valores que nos importan que son 10 entradas ignorando la intesidad de señal del EEG, estos valores irán dentro de una lista que entrarán a nuestra red neuronal la cual nos devolverá una salida binaria (1 ó 0) donde 1 hará que el brazo se mueva hacía la derecha y 0 que el brazo se mueva hacía la izquierda, esto ocurre gracias a que se establece una comunicación por medio del puerto serial y cuando se establece la comunicación este podrá recibir los valores antes mencionados, según los datos procesados.

Movimiento del brazo

El motor DC del brazo a controlar se mueve de 0 a 180 grados y de 180 a 0 grados osea derecha o izquierda. Para tomar el valor de la posición del brazo se utilizaron potenciómetros que fueron colocados a lado del motor DC para que nos digan por medio de ellos en que posición se encuentran.

Código del arduino:
Código del preprocesamiento:


Código de prueba de comunicación con arduino:

Control de versiones

http://github.com/SaulG/redesNeuronales

Reporte de laboratorio 6

B.12.2. Sea el sistema definido por

donde

Transforme las ecuaciones del sistema en la forma canónica observable.

1. Se tiene el planteamiento del problema original (1.1) y (1.2).

2. Se crea la función de transferencia del sistema de control (2).

3. Se crea la forma normal controlable apartir de su función de transferencia (3.1) y (3.2).

4. Se hace la transpuesta de la forma normal controlable y cambio de variables de B a C 

y de C a B, esto se hace para obtener la forma normal observable (4.1) y (4.2).

5. Al final verificamos que haya sido la misma función de transferencia(5).

Código en Octave:
El uso del código en octave y la verificación de que sean equivalente las funciones de tranferencia de cada forma usada:

Fuentes de ayuda:
http://www.engr.mun.ca/~millan/6825/canonicals.pdf

Reporte grupal sobre propiedades estructurales

Introducción

El sistema que se pretende controlar es el mismo que se tiene como proyecto final de esta materia. Para ello daré una breve explicación, mi proyecto trata de mover una pelota a cierta altura en el aire dentro de un tubo donde este será movido por un ventilador con un motor DC, gracias a un sensor ultrasonico este sabría hacia que altura moverse, osea que tanta potencia le daríamos al motor DC para que la pelota se eleve. Para ello reciclaremos el juguete que vemos abajo, conectando el motor DC y el sensor ultrasonico a un arduino que por medio de este haremos el control.

Reporte
Esta es su representación en la forma normal controlable.
Código en Octave:

Esta es su representación en la forma normal observable.
Código en Octave:

Esta es su representación en la forma de Jordan.
Código en Octave:

Código en Latex del documento:



Personas del equipo:

Saúl Gausin
Raúl Gonzalez
Isaías Garza

Problema 14.1 y 14.1.1

14.1 If a professor forgets coins or drink at the machine, there inmediately will be a student who will come to the machine.

Where P equivale a maestro, fcoin equivale si el maestro olvida monedas y fdrink si el maestro olvida bebida y SC equivale a que el estudiante vendrá.

14.1.1 If the beer storage becomes empty, it gets rechanged inmediately.

Donde BE equivale a almacenamiento vacío de cerveza y R es rechanged.

Problema de laboratorio

B.5.20. Obtenga la respuesta a una rampa unitaria del sistema definido por

donde u es una entrada rampa unitaria. Utilice el comando lsim para obtener la respuesta.

Código:


Gráfica: