P2.16. Obténgase un grafo de flujo de señal para representar el siguiente conjunto de ecuaciones algebraicas donde  y
y se consideran las variables dependientes y 6 y 11 son las
se consideran las variables dependientes y 6 y 11 son las
 y
y se consideran las variables dependientes y 6 y 11 son las
se consideran las variables dependientes y 6 y 11 son las
entradas:
Determínese el valor de cada variable dependiente usando la fórmula de la ganancia. Después, resuélvase para mediante mediante la fórmula de ganancia del flujo de señal de Mason y verifíquese la solución usando la regla de Cramer.
mediante la fórmula de ganancia del flujo de señal de Mason y verifíquese la solución usando la regla de Cramer.
 mediante la fórmula de ganancia del flujo de señal de Mason y verifíquese la solución usando la regla de Cramer.
mediante la fórmula de ganancia del flujo de señal de Mason y verifíquese la solución usando la regla de Cramer.
Grafo de flujo de señal:
Ganancia del flujo de señal:
Regla de Cramer:













































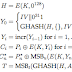
;04014806.jpg)