To start experimenting first we need the next code, made it by me.
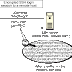
This is an image to demostrate how it works. Below of the image I explained more about the inputs and outputs of the program.
First we gave a message in this case I used '1111' with a noise ratio of 30%, then we encode the message and add some noise. We have message encoded in this case is '1011111' with an error in the second bit and the message corrected is '1111111', and just discarting the last 3 values then the real message transmitted is '1111'.
There are some errors detected in the current program the hamming code because the current code just can detect one error.
To solve this we can implement the extended hamming code, that just adding an extra bit of parity.
References
Encoding and Decoding with the Hamming Code










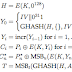



Pues, la experimentación no es exactamente exhaustiva y tampoco explicas cómo es capaz de corregir y cuántos errores. 4+3.
ResponderEliminar