Para realizar el proyecto, uno de los pasos importantes es verificar que nuestro sistema tenga estabilidad y para ello una manera de ver e identificar que nuestro sistema es realmente estable se pueden realizar distintos diagramas tales como diagrama de bode, respuesta y nyquist.
Primero veremos algo del código del cual es relativamente corto, con la ayuda de la librería de control se usaron las funciones para dibujar y representar la función de transferencia.
Recordando que nuestra función de transferencia es la siguiente:
Ahora veamos los diagramas que nos dio nuestro programa.
Diagrama de bode:
Diagrama de respuesta:
Diagrama de nyquist:
Conclusión
Tomando en cuenta la teoría de las definiciones del libro de control que se lleva en la materia, se puede decir que nuestro sistema es estable debido a que cumple con las siguientes características nuestro sistema en los diagramas anteriores, cumplen con un ligero cambio y no sufre de cambios bruscos, ademas los diagramas de respuesta cumplen con lo deseado, ya que la respuesta que se espera es ligero y no brusco. Basandome en una presentación donde muestra un sistema parecido me di cuenta que nuestro sistema cumple con algunas características típicas cuando se hace control de un motor dc.
martes, 30 de octubre de 2012
Sistema de Transiciones: Elevador
A continuación veremos mi sistema de transiciones que consiste en un elevador y una puerta, basandome en la entrada anterior en donde modele el mismo sistema hice el sistema de transiciones en donde también se corrigieron unos errores cometidos en el modelo de la red petri en donde nunca regresaba a un estado inicial.
Y este es el código que hice en promela basandome en la explicación de las diapositivas que dejaré debajo.
Fuente:
Diapositivas de promela.
Y este es el código que hice en promela basandome en la explicación de las diapositivas que dejaré debajo.
Fuente:
Diapositivas de promela.
domingo, 28 de octubre de 2012
Steganography Assignment
Here's my code in three of the six photos. I recommend to download these photos from the link below because blogspot changes something and it's difficult to recover the information.
After the deadline, I'm going to explain how my algorithm works.
Parameters to encrypt:
1.- Name of the text to encrypt
2.- The image to hide the message
3.- The name of the image with the message
Example:
imagenes.py photo8.bmp copia8.bmp
Parameters to decrypt:
1.- Name of the image with the message
2.- The file to put the message
3.- The keyword "decripta"
Example:
copia6.bmp recuperado6.dat decripta
Código
**Note** The three images with message are the number 1, 3 and 5.
jueves, 25 de octubre de 2012
Stream ciphers: Trivium
What is Trivium?
Trivium is a hardware oriented synchronous stream cipher, that was designed as an exercise in exploring how far a stream cipher can be simplified without sacrificing its security, speed or flexibility.
Trivium is a synchronous stream cipher designed to generate up to 2 ^64 bits of key stream from an 80-bit secret key and an 80-bit initial value (IV), the process consists of two phases: first the interntal state of the cipher is initialized using the key and the IV, then the state is repeatedly updated and used to generate key stream bits. These are the parameters:
Key size: 80 bit
IV size: 80 bit
Internal state: 288 bit
Who invented Trivium?
It was submitted to a eSTREAM competition by its authors, Christophe De Cannière and Bart Preneel, and has been selected as part of the portfolio for low area hardware ciphers by the eSTREAM project, It's not patented.
How does It work?
Key stream generation; The proposed design contains a 288-bit internal state denoted by (s 1, ..., s 288). The key stream generation consists of an iterative process which extracts the values of 15 specific state bits and uses them both to update 3 bits of the state and to compute 1 bit of key stream z i. The state bits are then rotated and the process repeats itself until the requested N <= 2 ^64 bits of keys stream have been generated. Here is a pseudo-code:
Where "+" and "." operations stand for addition and multiplication over GF(2), which is the Galois Field of two elements (XOR and AND).
Key and IV setup; the algorithm is initialized by loading an 80-bit key and an 80-bit IV into the 288-bit initial state, and setting all remaining bits to 0, except for s ^286, s ^287 and 2 ^288, then the state is rotated over 4 full cycles without generating key stream bits.
Key and IV setup; the algorithm is initialized by loading an 80-bit key and an 80-bit IV into the 288-bit initial state, and setting all remaining bits to 0, except for s ^286, s ^287 and 2 ^288, then the state is rotated over 4 full cycles without generating key stream bits.
Attacks known
There are some attacks known as you can see below:
Source:
Article where you can see specifications.
Article Algebraic Attack
http://www-polsys.lip6.fr/~jcf/Papers/SCC08c.pdf
Two Trivial Attacks on Trivium
https://www.cosic.esat.kuleuven.be/ecrypt/stream/papersdir/2007/006.pdf
Cube Attacks on Trivium
http://eprint.iacr.org/2009/015.pdf
martes, 23 de octubre de 2012
Redes Petri: Elevador
El sistema que modele fue el de un elevador, en donde lo separé en dos componentes: Puerta y Elevador, en donde Puerta tiene como estados Abierto y Cerrado en el cual como el nombre lo dice en el estado Abierto abre la puerta del elevador y Cerrado cierra la puerta de la misma, como transiciones tenemos una comparación de unas variables boleanos donde verifica si el elevador le manda la señal de ascender o descender, en donde sí recibe un valor verdadero este mantiene cerrada la puerta. En Elevador tenemos 4 estados Inicio, Subir, Bajar y Detener, donde Inicio es cuando el elevador esta por usarse y nos envía la variable Piso según el piso elegido a una transición Piso > Actual ó Piso < Actual, el cual la primera irá hacía Subir y la segunda hacía Bajar todo esto hasta que Piso sea igual al Actual para entrar a el estado Detener.
Redes Petri:
Código:
Redes Petri:
Código:
jueves, 18 de octubre de 2012
Galois/Counter Mode(GCM)
What is GCM?
GCM is a block cipher mode of operation providing both
confidentiality and data origin authentication; It is defined for block
ciphers with block sizes of 128, 192 and 256 bits. Galois Message
Authentication Code (GMAC) is an authentication-only variant of the GCM
which can be used as an incremental message authentication code. Both
GCM and GMAC can accept initialization vectors of arbitrary length.
Who invented GCM?
GCM was designed by McGrew and Viega as an improvement to Carter-Wegman Counter CWC mode. On November 26, 2007 NIST announced the release of NIST Special Publication Recommendation for Block Cipher Modes of Operation: Galois/Counter Mode (GCM) and GMAC making GCM and GMAC official standards.
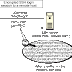
These are the Inputs and Outputs for GCM system
GCM has two operations, authenticated encryption and authenticated decryption, where the authenticated encryption has four inputs, and each of which is a bit string:
- A secret key K, whose length depends of the block cipher use.
- An initialization vector IV, that can have any number of bits between 1 and 2 ^64. For a fixed value of the key, each IV value must be distinct. If you are looking for efficiency is recommended 96-bit IV values.
- A plaintext P, which can have any number of bits between 0 and 2 ^39 -256.
- Additional authenticated data (AAD), which is denoted as A, this data is authenticated, but not encrypted, and can have any number of bits between 0 and 2 ^64.
There are two outputs:
- A ciphertext C whose length is exactly that of the plaintext P.
- An authentication is denotated as T, whose length can be any value between 0 and 28. The length is denotated as t.
How does It work?
First we have to know the notation
The two main functions used in GCM are block cipher encryption and multiplication over the field GF(2 ^128). The block cipher encryption of the value X with the key K is denoted as E(K, X). The multiplication of two elements X, Y ∈ GF(2 ^128) is denoted as X · Y , and the addition of X and Y is denoted as X ⊕ Y . A, the addition in this field is equivalent to the bitwise exclusive-or operation.
The function len() returns a 64-bit string containing the nonnegative integer describing the number of bits in its argument, with the least significant bit on the right. The expression 0l denotes a string of l zero bits, and AkB denotes the concatenation of two bit strings A and B. The function MSBt(S) returns the bit string containing only the most significant (leftmost) t bits of S, and the symbol {} denotes the bit string with zero length.
Now Let's know how it works...
Encryption
Let n and u denote the unique pair of positive integers such that the total number of bits in the plaintext is (n − 1) 128 + u, where 1 ≤ u ≤ 128.
The plaintext consists of a sequence of n bit strings, in which the bit length of the last bit string is u, and the bit length of the other bit strings is 128. The sequence is denoted P 1, P 2, ...,P n-1, P ∗ n, and the bit strings are called data blocks, although the last bit string, P ∗ n, may not be a complete block. Similarly, the ciphertext is denoted as C 1, C 2,...,C n − 1 ,C ∗ n, where the number of bits in the final block C ∗ n is u. The additional authenticated data A is denoted as A 1, A 2,..., A m − 1, A ∗ m, where the last bit string A ∗ m may be a partial block of length v, and m and v denote the unique pair of positive integers such that the total number of bits in A is (m − 1) 128 + v and 1 ≤ v ≤ 128.
The authenticated encryption operation is defined by the following equations:
The plaintext consists of a sequence of n bit strings, in which the bit length of the last bit string is u, and the bit length of the other bit strings is 128. The sequence is denoted P 1, P 2, ...,P n-1, P ∗ n, and the bit strings are called data blocks, although the last bit string, P ∗ n, may not be a complete block. Similarly, the ciphertext is denoted as C 1, C 2,...,C n − 1 ,C ∗ n, where the number of bits in the final block C ∗ n is u. The additional authenticated data A is denoted as A 1, A 2,..., A m − 1, A ∗ m, where the last bit string A ∗ m may be a partial block of length v, and m and v denote the unique pair of positive integers such that the total number of bits in A is (m − 1) 128 + v and 1 ≤ v ≤ 128.
The authenticated encryption operation is defined by the following equations:
Successive counter values are generated using the function incr(), which treats the rightmost 32 bits of its argument as a nonnegative integer with the least significant bit on the right, and increments this value modulo 2 ^32. More formally, the value of incr(F||I) is F||(I + 1 mod 2 ^32).
The function GHASH is defined by GHASH(H,A,C) = X m + n + 1, where the
inputs A and C are defined as we defined in the beginning, and the
variables X i for i = 0,...,m + n + 1 are defined below:
Below we can see the process of encryption.
Decryption
The authenticated decryption operation is similar to the encrypt operation, but with the order of the hash step and encrypt step reversed, as you can see below how it works by the following ecuations:
Multiplication in GF(2 ^128)
The multiplication operation is defined as an operation on bit vectors in order to simplify the specification, this corresponds to the particular field representation used in GCM. Each element is a vector of 128 bits, the i th bit of an element X is denoted as X i; The leftmost bit is X 0, and the rightmost bit is X 127.
The multiplication operation uses the special element R = 11100001 || 0 ^120; The function rightshift() moves the bits of its argument one bit to the right, in other words whenever W = rightshift(V), then W i = V i-1 for 1 ≤ i ≤ 127 and W 0 = 0. We can see it illustrated below.
The Field GF(2 ^128)
A finite field is defined by its multiplication and addition operations. These operations obey the basic algebraic properties that one expects from multiplication and addition (commutativity, associativity, and distributivity). Both operations map a pair of field elements onto another field element. In a polynomial basis,the multiplication of two elements X and Y consists of multiplying the polynomial representing X with the polynomial representing Y, then dividing the resulting 256-bit polynomial by the field polynomial; the 128-bit remainder is the result. GCM uses the following polynomial:
The addition of two elements X and Y consists of adding the polynomials together, because each coefficient is added independently, and the coefficients are in GF(2), this operation is identical to the bit wise exclusive-or of X and Y. No reduction operation is needed. Subtraction over GF(2 ^128) is identical to addition, because the field GF(2) has that property.
Attacks known
I find some information about his weaknesses in the GMAC (Galois Message
Authentication Code), well actually this is a common weak in all kind of encryption or decryption that needs a key. You have to use a value relative prime.
Sources:
Problema de laboratorio
B.6.7 Dibuje los lugares de los raices para un sistema de control en lazo cerrado con:
Comandos en Octave usando la librería control:
Dibujado:
Comandos en Octave usando la librería control:
Donde la función tf nos ayuda a crear o convertir un modelo de una función de transferencia, rlocus nos ayuda a graficar nuestro sistema en "lugar de raíces".
martes, 16 de octubre de 2012
Lógica predicativa: Red Wireless
En esta entrada hablaremos sobre teoría de grafos aplicada en lógica de primer orden, para ello nos enfocaremos en redes wireless para reducir las interferencias en las redes wireless.
El problema de reducir la interferencia en redes resulta ser muy difícil, y por esta razón, se han investigado diseños de topologías talescomo, multi-hop, red triangular, la unidad gráficos de disco, hexagonal, entre otros.
Los aspectos clave del problema de interferencia en las redes inalámbricas podría ser una solución artificial en un entorno distribuido o centralizado, hace unos pocos meses salió a la luz una investigación que realizaron unos científicos de la Universidad de Catalunya sobre el canto que realizaban unas ranas macho donde ellos los realizan poder atraer a las hembras así reconocen el origen de la llamada y localizan al pretendiente, el problema surge cuando dos machos están demasiado cerca y cantan a la vez.
Las hembras quedan confundidas y no pueden determinar de donde proceden las llamadas, por lo que los machos han tenido que aprender a desincronizar sus cantos. El objetivo de esta investigación es realizar un sistema inteligente que realize el comportamiento de las ranas para que esto ayude a hacer operaciones distribuidas.
Una de las cosas que más se realizan son simulaciones donde se pueden trazar los metros cuadrados donde se piensa implementar el sistema y dejar que el sistema haya lo suyo donde tome como parámetros las propiedades de las antentas y la cantidad de ellas.
Fuentes:
http://www.agenciasinc.es/Noticias/El-canto-de-una-rana-inspira-un-algoritmo-para-redes-inalambricas
El problema de reducir la interferencia en redes resulta ser muy difícil, y por esta razón, se han investigado diseños de topologías talescomo, multi-hop, red triangular, la unidad gráficos de disco, hexagonal, entre otros.
Los aspectos clave del problema de interferencia en las redes inalámbricas podría ser una solución artificial en un entorno distribuido o centralizado, hace unos pocos meses salió a la luz una investigación que realizaron unos científicos de la Universidad de Catalunya sobre el canto que realizaban unas ranas macho donde ellos los realizan poder atraer a las hembras así reconocen el origen de la llamada y localizan al pretendiente, el problema surge cuando dos machos están demasiado cerca y cantan a la vez.
Las hembras quedan confundidas y no pueden determinar de donde proceden las llamadas, por lo que los machos han tenido que aprender a desincronizar sus cantos. El objetivo de esta investigación es realizar un sistema inteligente que realize el comportamiento de las ranas para que esto ayude a hacer operaciones distribuidas.
Una de las cosas que más se realizan son simulaciones donde se pueden trazar los metros cuadrados donde se piensa implementar el sistema y dejar que el sistema haya lo suyo donde tome como parámetros las propiedades de las antentas y la cantidad de ellas.
Fuentes:
http://www.agenciasinc.es/Noticias/El-canto-de-una-rana-inspira-un-algoritmo-para-redes-inalambricas
martes, 9 de octubre de 2012
Diagrama de bloques
Para esta entrada hablaremos sobre el diagrama de bloques en nuestro proyecto, en sí el proyecto consiste en mover una pelota a cierta altura en el aire dentro de un tubo donde este será movido por un ventilador con un motor DC, gracias a un sensor ultrasonico este sabría hacia que altura moverse, osea que tanta potencia le daríamos al motor DC para que la pelota se eleve. Para ello reciclaremos el juguete que vemos abajo, conectando el motor DC y el sensor ultrasonico a un arduino que por medio de este haremos el control.
Fuente de la imágen: http://maxkalavera.blogspot.mx/2012/10/diagramas-de-bloque-yo-flujo-de-senales.html
Una vez explicado lo anterior procederemos al diagrama de bloques:
Fuente de la imágen: http://maxkalavera.blogspot.mx/2012/10/diagramas-de-bloque-yo-flujo-de-senales.html
Una vez explicado lo anterior procederemos al diagrama de bloques:
lunes, 8 de octubre de 2012
Reporte de proyecto de medio curso
A continuación presentaré los avances que se han realizado en el proyecto desde el código hasta el hardware. Antes de comenzar a explicar sería bueno recordar de que trata mi proyecto, la idea del proyecto es hacer una red neuronal que por medio de unos
electrodos en el antebrazo de una persona determine los movimientos que
quiere realizar en el brazo, esto se puede por medio de frecuencias que
manda el cerebro hacia el brazo, y lo que se busca es interceptar esas
frecuencias en el antebrazo, para poder controlar un brazo robótico
aunque lo ideal sería primero simularlo.
Comparado lo propuesto con lo actual que se tiene avanzado, se están tomando en cuenta solamente un motor DC del brazo a controlar para este avance donde el brazo se mueve de 0º a 180º y de 180º a 0º.
Ahora mostaré una imágen del brazo robótico,
El sensor utilizado fue un EMG con la ayuda de un arduino y unos cables que conectan a unos electrodos que nos facilitan la lectura de datos del músculo,
para más información sobre que es un EMG vayan a esta página http://es.wikipedia.org/wiki/Electromiografía y para datos relacionados al sensor podrían ir a esta página
https://docs.google.com/file/d/0B8Wy2qiwirwyWnBkM09JT29LaXM/edit
donde muestra el manual de uso del mismo.
Por parte del código que nos ayuda a comunicar el brazo donde toma como salida el resultado de la red neuronal es el siguiente:
El código es tan simple como se explica en los comentarios, entendiendo eso y el siguiente que es el que normaliza los datos de entrada del sensor pasaremos a ver el código de la red neuronal.
Ahora veremos el código de la red neuronal.
El control de versiones del proyecto puede ser accedido a través de esta liga:
Pruebas con las neuronas:
**ACTUALIZADO** 9/10/2012 9:28AM Actividad de los commits
Comparado lo propuesto con lo actual que se tiene avanzado, se están tomando en cuenta solamente un motor DC del brazo a controlar para este avance donde el brazo se mueve de 0º a 180º y de 180º a 0º.
Ahora mostaré una imágen del brazo robótico,
El sensor utilizado fue un EMG con la ayuda de un arduino y unos cables que conectan a unos electrodos que nos facilitan la lectura de datos del músculo,
para más información sobre que es un EMG vayan a esta página http://es.wikipedia.org/wiki/Electromiografía y para datos relacionados al sensor podrían ir a esta página
https://docs.google.com/file/d/0B8Wy2qiwirwyWnBkM09JT29LaXM/edit
donde muestra el manual de uso del mismo.
Por parte del código que nos ayuda a comunicar el brazo donde toma como salida el resultado de la red neuronal es el siguiente:
El código es tan simple como se explica en los comentarios, entendiendo eso y el siguiente que es el que normaliza los datos de entrada del sensor pasaremos a ver el código de la red neuronal.
Ahora veremos el código de la red neuronal.
El control de versiones del proyecto puede ser accedido a través de esta liga:
Pruebas con las neuronas:
**ACTUALIZADO** 9/10/2012 9:28AM Actividad de los commits
Suscribirse a:
Comentarios (Atom)














































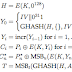
;04014806.jpg)